Programmers1 Lv.2 '유사 칸토어 비트열' 파이썬 코드 및 풀이

조건 파악
유사 칸토어 비트열의 길이는 5^n 이므로 최대 13자리 수이다. 한편, r < l + 10,000,000은 r - l < 10,000,000이므로 하다못해 l부터 r사이의 구간만 탐색한다 해도 그 길이가 최대 10^7이다.
따라서 이 문제는 시간복잡도 O(N)만에 풀어야 한다. 유사칸토어비트열을 구하고 또 구간을 탐색하면 시간초과가 발생할 것이다.
접근
풀이의 목적은 유사 칸토어 비트열을 구하는 게 아니라 특정 구간의 1의 개수를 알아내는 것이다. 패턴을 파악하면 비트열을 구하지 않아도 개수를 알 방법이 있을 것이다.
한편, 1의 개수를 구하는 함수를 count(from,to)라고 할 때 count(l,r)은 count(0,r) - count(0,l)과 같다. 따라서 특정 지점까지의 1의 개수만 구하자.

유사 칸토어 비트열의 길이는 5^n이며 맨앞의 5^(n-1)의 길이를 가지는 부분은 n-1번째 유사칸토어비트열과 같다.
가장 중요한 것은 길이가 5의 제곱수일 때 패턴이 만들어지고 해당 패턴 안의 1의 개수는 4의 제곱수라는 것이다.
특정 위치까지의 1의 개수를 구하고자 한다면 해당 위치 앞에 패턴이 몇 개 나왔는지 알면 된다. 위치를 가리키는 수를 5의 제곱수로 나누면서 나머지를 알아보면 된다. 그리고 이것은 10진수를 5진수로 바꾸는 과정과 일치한다.
예시
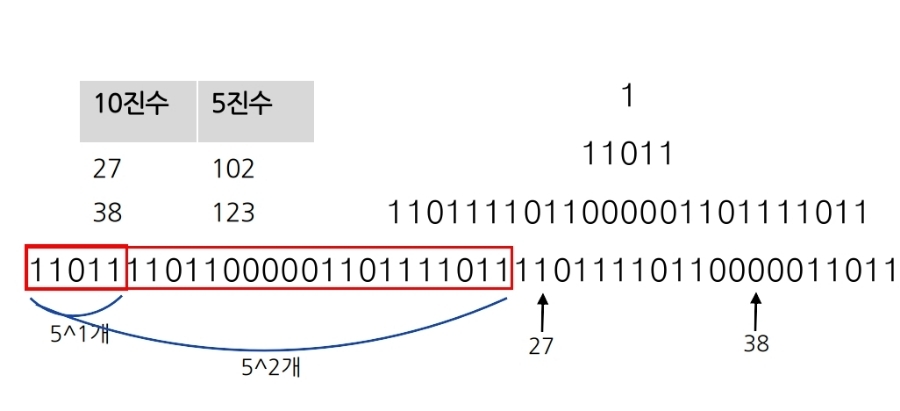
27을 5진수로 바꾸면 102이며 앞에 나오는 패턴의 수는 길이 5^2인 패턴이 1개, 5^1인 패턴이 0개, 그리고 나머지가 2이다. 각 패턴은 1을 4^n개 만큼 갖고 있다. 따라서 1의 개수는 4^2 * 1 + 2 = 18이다.
38을 5진수로 바꾸면 123이며 앞에 나오는 패턴의 수는 길이 5^2인 패턴이 1개, 5^1인 패턴이 2개, 그리고 나머지가 3이다. 그러나 이 경우는 38번째 자리가 0을 가리키고 있다. 마지막 자리숫자 3의 의미가 바뀌게 된다.
크던 작던 어떤 패턴이 두 번 반복된 다음에는 반드시 0이 몰려있는 구간이 나오는 것을 알 수 있다. 이러한 예외를 해결하기 위해 두 가지 조작을 해야한다.
1. 5진수의 각 자리에 올 수 있는 숫자 {0,1,2,3,4}를 {0,1,2,2,3}에 대응 시킨다. 중간의 공차를 하나 빼는 것이다.
2. 5진법으로 바꾼 수의 어떤 자리의 숫자가 2이면 그 아래 자리 숫자들은 모두 0으로 처리한다.
다시 38의 예시로 돌아와서 5진수 123을 120으로 바꾸게 되면 4의 제곱수로 1의 개수를 정확히 셀 수 있게 된다.
의사코드
l-1,r을 5진수로 바꾼다 (폐구간이므로 l 대신 l-1)
2가 나오는 가장 큰 자리의 수 다음 숫자들을 모두 0으로 바꾼다.
{0,1,2,3,4}를 {0,1,2,2,3}에 대응한다
4진법이라 생각하고 다시 10진수로 바꾼다.
각각의 차를 구한다.
이렇게 하면 시간복잡도 O(1)의 상수시간 만에 답을 구할 수 있다.
구현
def solution(n, l, r):
q_l = quin(l - 1)
q_r = quin(r)
count_l = decode(q_l)
count_r = decode(q_r)
return count_r - count_l
def quin(n) :
result = []
while n > 0 :
n,mod = divmod(n,5)
result.append(mod)
return result[::-1]
def decode(quinary) :
result = 0
length = len(quinary)
dec = [0, 1, 2, 2, 3]
for i, x in enumerate(quinary) :
exponent = length-i-1
result += (4**exponent)*dec[x]
if x == 2 :
break
return result'Software Engineering' 카테고리의 다른 글
| Multi-modality와 범용 멀티모달 모델 BEiT-3의 간단한 소개 (0) | 2023.03.06 |
|---|---|
| vscode.dev에서 원격 Jupyter 서버 연결하기 (0) | 2023.03.05 |
| [Python 문제 풀이] 프로그래머스 '호텔 대실' (0) | 2023.02.17 |
| [Python 문제 풀이] 프로그래머스 '빛의 경로 사이클' (0) | 2023.02.09 |
| AJAX 옵션 정리 (0) | 2021.04.06 |