반응형
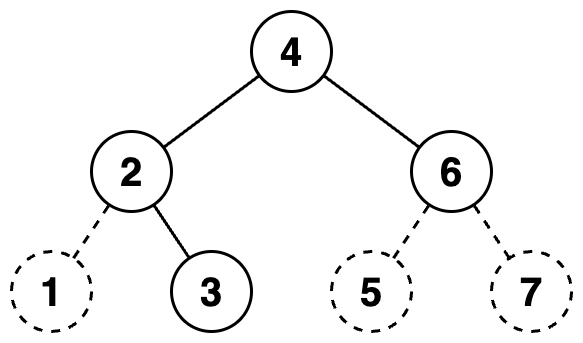
포화 이진트리의 노드 수는 2^n - 1이다.
programmers lv2 파이썬 표현 가능한 이진트리
접근
이진트리로 표현가능하기 위해선 중간에 끊긴 부분이 없어야 한다. 부모노드가 없이 자식노드가 있다면 하나의 이진트리로 표현 불가능할 것이다. 해당 부분을 체크하면서 탐색하면 되겠다.
numbers의 원소는 최대 10^15 이며 leaf nodes를 제외한 모든 노드를 검사한다고 하면 (10^15- 1)/2이고 numbers의 길이는 10,000이다. 따라서 N의 크기는 (10^19-10^4)/2이며 전체탐색으로 풀 수 없는 크기이다. 근데 이게 된다. 입력값을 어느정도 제한해놓았을 것이라 생각한다.
의사코드
1. 이진수로 바꾼다
2. 포화이진트리를 표현하기 위해 2^n-1의 길이가 되도록 앞에 '0'을 추가한다.
3. 루트에서 차례대로 자식노드를 탐색해 나간다.
구현
import math
def solution(numbers):
answer = []
for number in numbers :
available = 1 #default
# Change it to binary
b = bin(number)[2:]
# Add zeros left in order to make it full-binary tree
if not isinstance(math.log2(len(b)+1),int) :
full_length = 2**math.ceil(math.log2(len(b)+1)) - 1
b = '0'*(full_length-len(b)) + b
# Add one element at left in order to make its 2^n length
b = '_' + b
# Initial values for loop
root = int(len(b)/2)
parents = [root]
children = []
i = int(root/2)
# Start searching
while i>=1 : # if i < 1 , it has been finished searching leaf nodes.
for n in parents :
# If there is child node without parent node, it's unavailable.
if b[n] == '0' and '1' in [b[n-i],b[n+i]] :
available = 0
break
break
else : # Stack children to search again from them.
children.extend([n-i,n+i])
parents = children
children = []
i = int(i/2)
answer.append(available)
return answer최악의 경우
numbers의 원소의 최대크기는 10^15이며 2^49 < 10^15 < 2^50이다. 따라서 최악의 경우의 입력은 1로만 채워진 2^50-1자리의 2진수를 10진수로 표현한 값이다. 이를 입력으로 테스트를 진행해보았다.
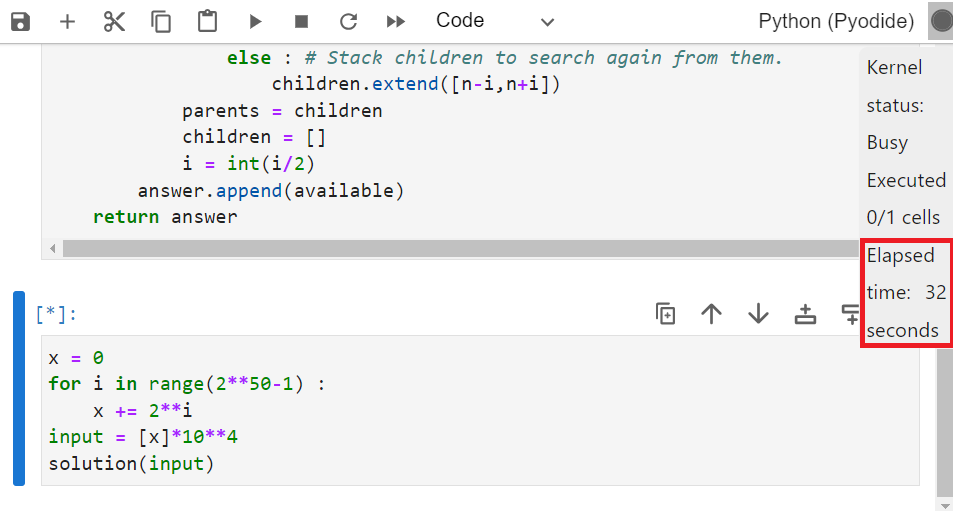
노트북 배터리모드에서 30초가 넘어갔는데 더 볼 필요도 없다. 도저히 몇 초만에 풀 수 없는 문제이다.
반응형
'Software Engineering' 카테고리의 다른 글
| [Python 문제 풀이] 프로그래머스 '표 병합' (0) | 2023.08.19 |
|---|---|
| DataProc vs DataFlow (0) | 2023.08.18 |
| [Python 문제 풀이] 프로그래머스 '인사고과' (0) | 2023.06.27 |
| [Python 문제 풀이] 프로그래머스 '부대 복귀' (0) | 2023.06.15 |
| [Python 문제풀이] 프로그래머스 '연속 펄스 부분 수열의 합' (0) | 2023.06.14 |